Example 1. If ![]() and
and ![]() are positive numbers and
are positive numbers and 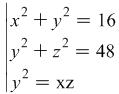 then without finding the values for
then without finding the values for ![]() and
and ![]() find the value of the expression
find the value of the expression ![]()
Solution: If we have to solve this system it would be easy for anyone manage to find ![]() and
and ![]() but in this problem
but in this problem ![]() is to be found. The system can be written down in the form
is to be found. The system can be written down in the form
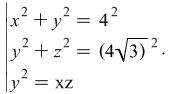
|
Since ![]() and
and ![]() are positive, from the first equation
are positive, from the first equation ![]() and
and ![]() can be considered using a reverse Pythagorean theorem as the lengths respectively of the legs and the hypotenuse in a right triangle ABD
can be considered using a reverse Pythagorean theorem as the lengths respectively of the legs and the hypotenuse in a right triangle ABD ![]() (fig.1)
(fig.1)
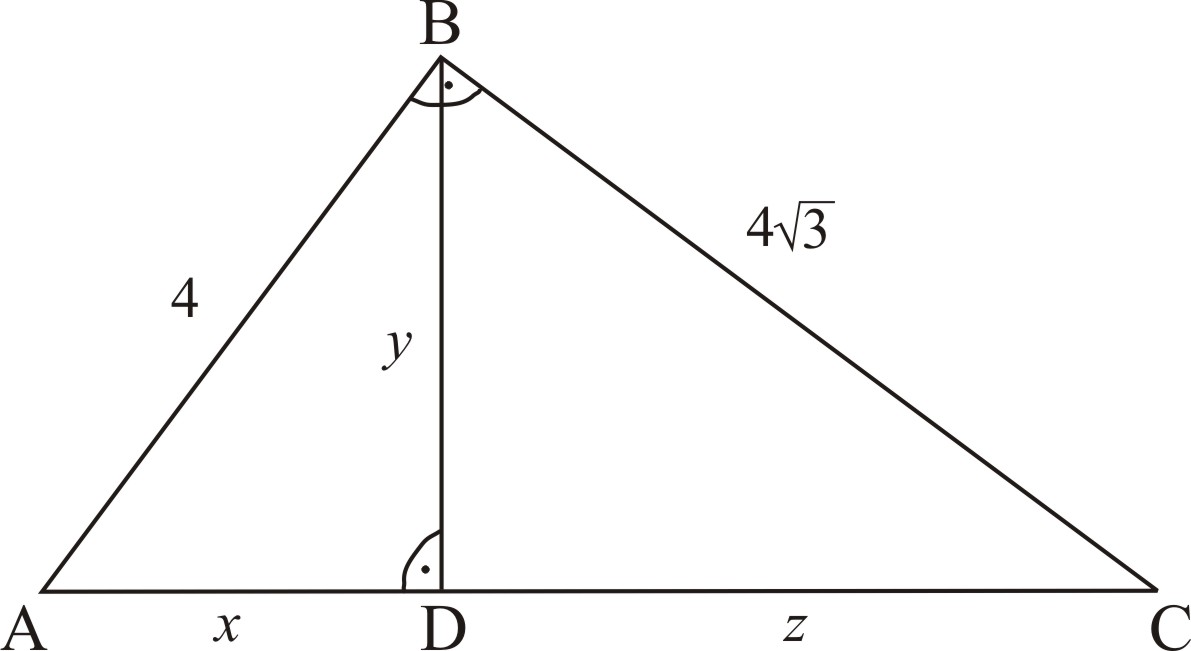 |
| Figure 1. |
If we consider the second equation of the system we can reach an analogical conclusion ![]() и
и ![]() are the respective lengths of the legs and hypotenuse in a triangle BCD
are the respective lengths of the legs and hypotenuse in a triangle BCD ![]() (fig.1).
(fig.1).
From the third equation we can make the conclusion that y is a number which is a geometrical average of ![]() and
and ![]() , and using the reverse theorem for proportional line segments in a right triangle the consequence is that
, and using the reverse theorem for proportional line segments in a right triangle the consequence is that ![]()
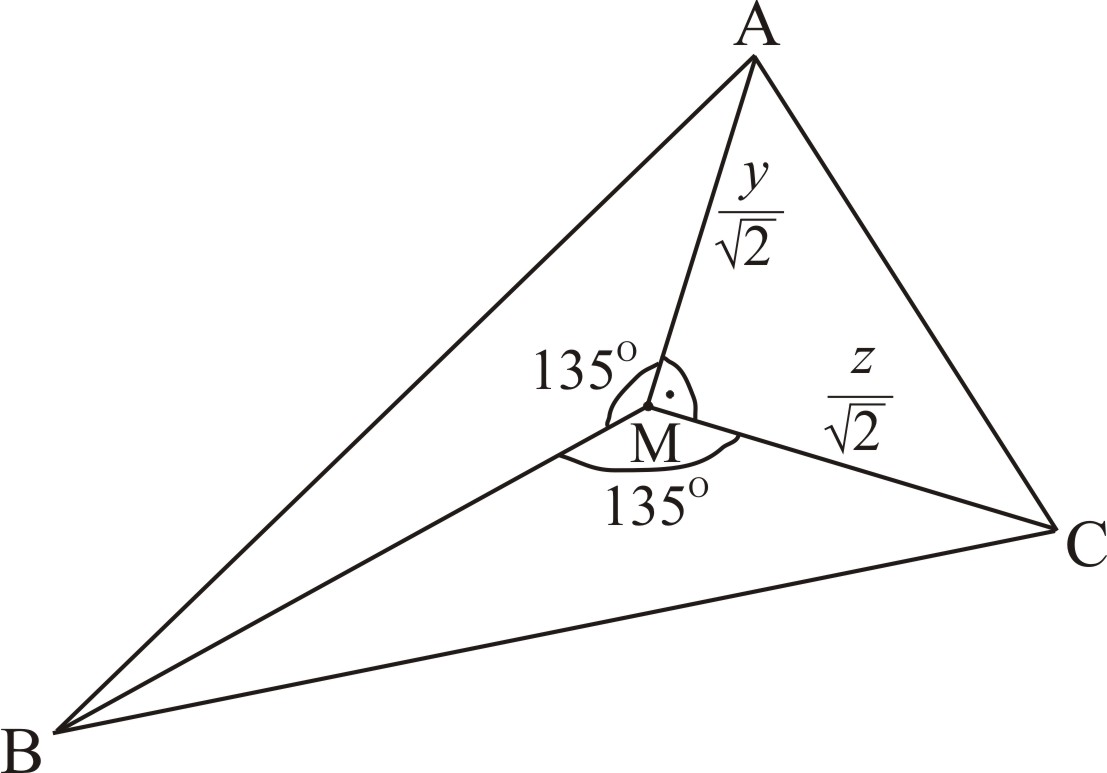
Now we examine the expression ![]() , which can be represented as
, which can be represented as ![]() . Considering figure 1
. Considering figure 1 ![]() but
but ![]()
In this way we find out that ![]() i.e.
i.e. ![]()
For this problem the question could be to find ![]() .
.

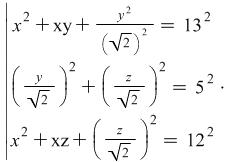
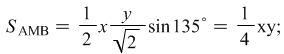
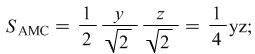
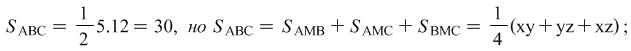
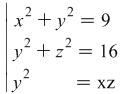 then without finding the values of
then without finding the values of 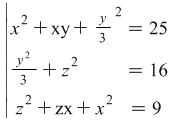
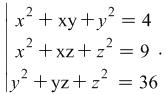


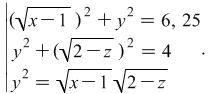
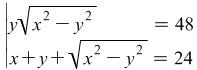 .
.